Research
Cellular Signaling: Information Theory, Bacterial Chemotaxis, and GPCRs
How do cells regulate their behavior based on complex environmental signals? This question arises in a wide range of scenarios, from bacterial chemotaxis to physiological responses in multicellular organisms. Receptors play a crucial role in detecting these signals, which are transmitted via the activation of intracellular messenger proteins that in turn initiate appropriate cellular responses. Our research focuses on signaling as a many-body nonequilibrium process: how do collections of interacting receptors, coupled to nonequilibrium chemical reaction networks, allow cells to effectively propagate information?
Recent experiments, combined with our theoretical work, have demonstrated a new paradigm for our understanding of cellular signaling, highlighting the importance of nonequilibrium driving and cooperative interactions. We have developed nonequilibrium allosteric and nonequilibrium lattice models of the chemosensory array in E. coli that have demonstrated the key role of energy dissipation in enhancing response speed, sensitivity and robustness as well as the adaptive range of chemosensory signaling.
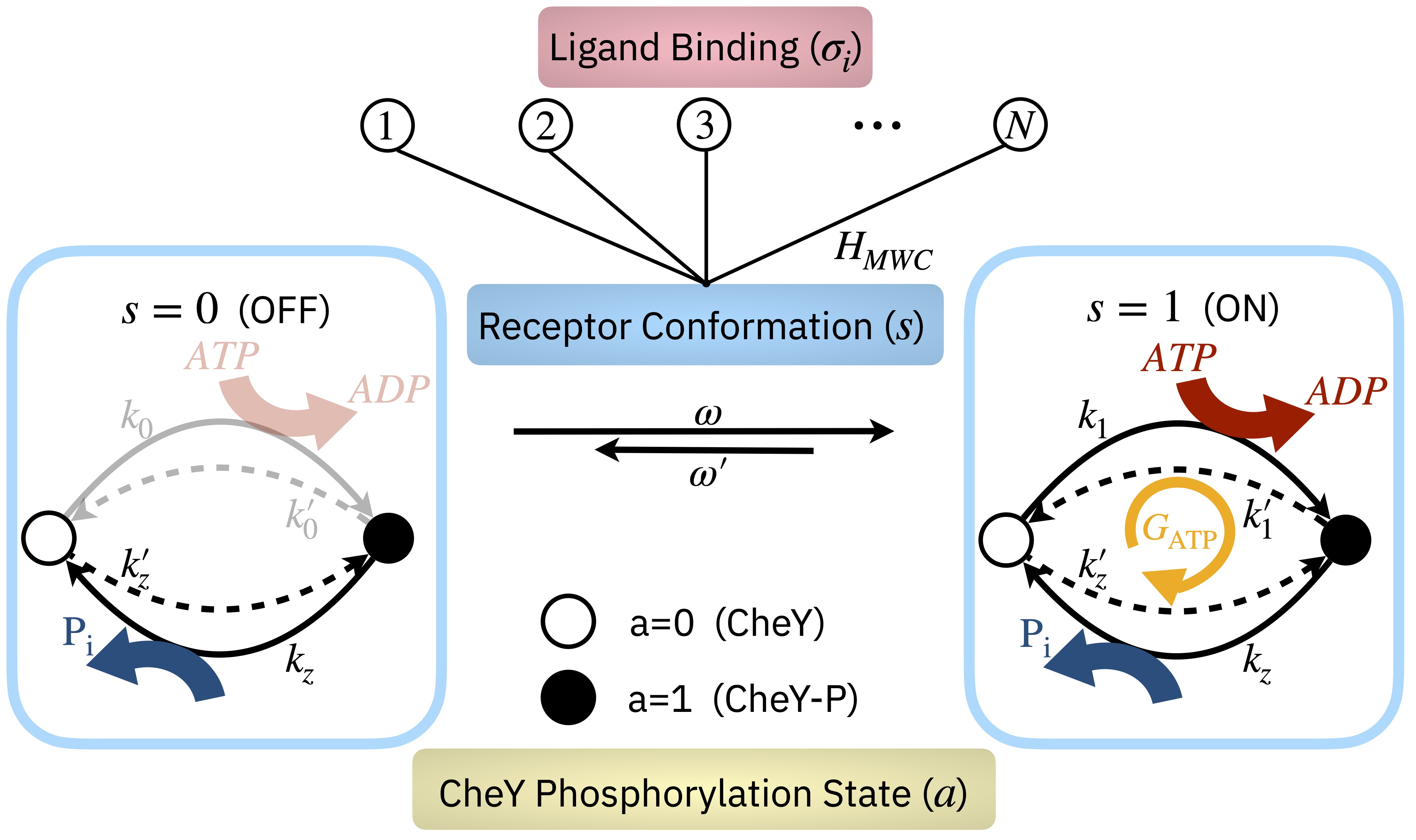
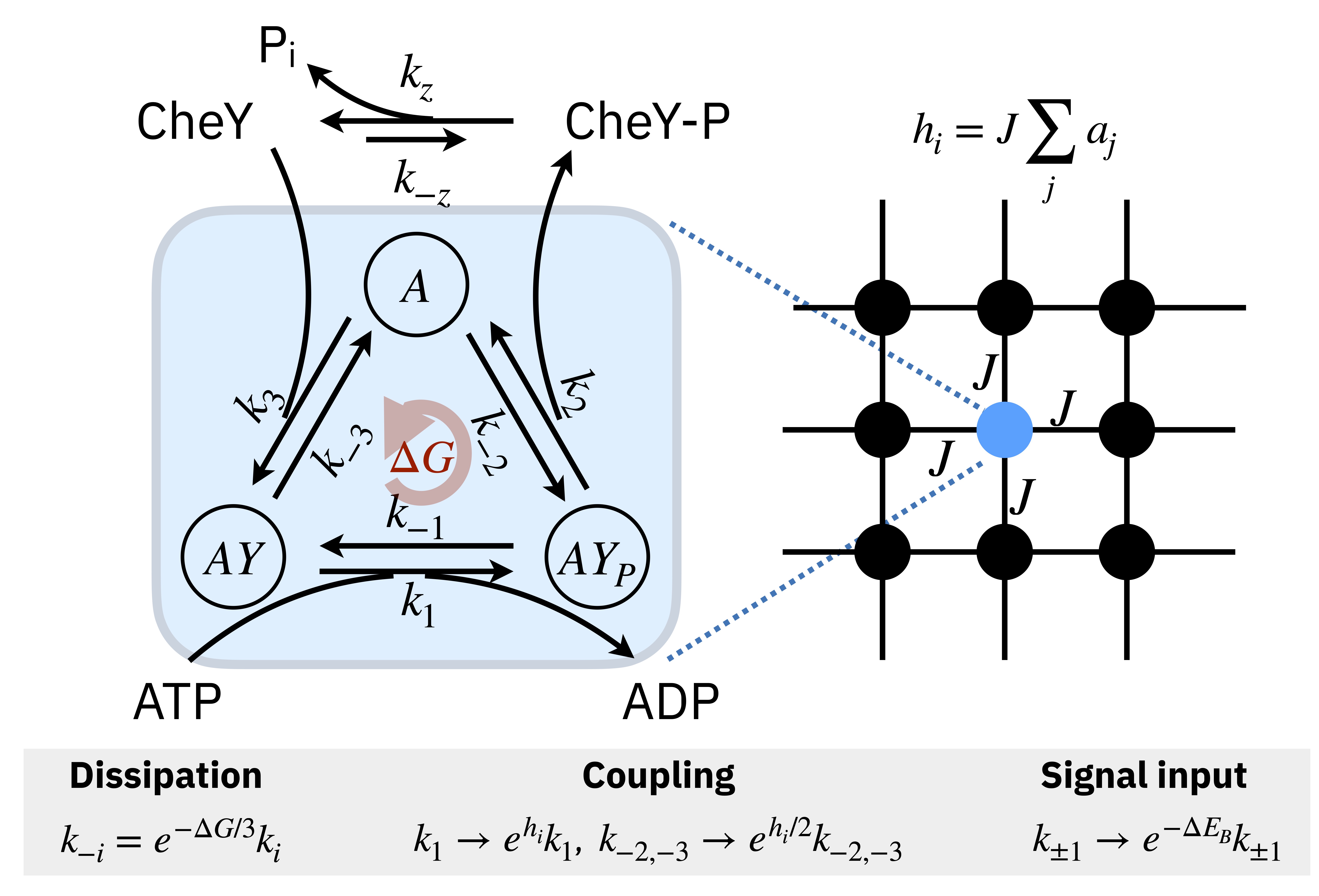
Ongoing research in the group aims to develop increasingly detailed nonequilibrium statistical mechanics models of the bacterial chemosensory array to study structure-function relationships, signaling heterogeneity, and the microscopic mechanisms underlying adaptation. We are also starting to apply a similar modeling approach to study oligomerization and signaling responses of G-protein coupled receptors (GPCRs), in collaboration with the Gradinaru lab at the University of Toronto.
Read more:
- D. Hathcock*, Q. Yu*, and Y. Tu, "Time-reversal symmetry breaking in the chemosensory array reveals a general mechanism for dissipation-enhanced cooperative sensing," Nat. Commun. 15, 8892 (2024). [PDF] [SI]
- D. Hathcock*, Q. Yu*, B.A. Mello, D.N. Amin, G.L. Hazelbauer, and Y. Tu, "A nonequilibrium allosteric model for receptor-kinase complexes: The role of energy dissipation in chemotaxis signaling," Proc. Natl. Acad. Sci. 120, e2303115120 (2023). [PDF] [SI]
- C. Weisenberger*, D. Hathcock*, and M. Hinczewski, "Cellular signaling beyond the Wiener-Kolmogorov limit," J. Phys. Chem. B 125, 12698 (2021). [PDF] [SI]
- D. Hathcock, J. Sheehy, C. Weisenberger, E. Ilker, and M. Hinczewski, "Noise Filtering and Prediction in Biological Signaling Networks," IEEE Trans. Mol. Biol. Multi-Scale Commun. 2, 16 (2016). [PDF]
Phase Transitions and Bifurcations
Many-body systems exhibit emergent phenomena: collections of spins, oscillators, or switches can organize into macroscopic collective phases: e.g. ordered vs disordered, synchronized vs desynchronized. Statistical physics and renormalization group theory predict that transitions between these phases exhibit universal scaling laws that are independent of microscopic details. We have developed techniques, built on a normal form theory for RG flows, to extend scaling theories beyond the critical region, enabling quantitative theories for thermodynamic properties over the entire phase diagram.
In a parallel line of research, we have leveraged normal forms to demonstrate that bifurcations serve as an organizing principle underlying soft robotics design. We developed a framework for tuning the dynamics of a magneto-elastic robot toward a high-order bifurcation, which allowed us to design transitions between multiple configurational states with only a few control parameters. This remains an active area of research, we are investigating the design of multi-state landscapes using many identical subunits, in collaboration with the Griniasty group at Tel Aviv University.
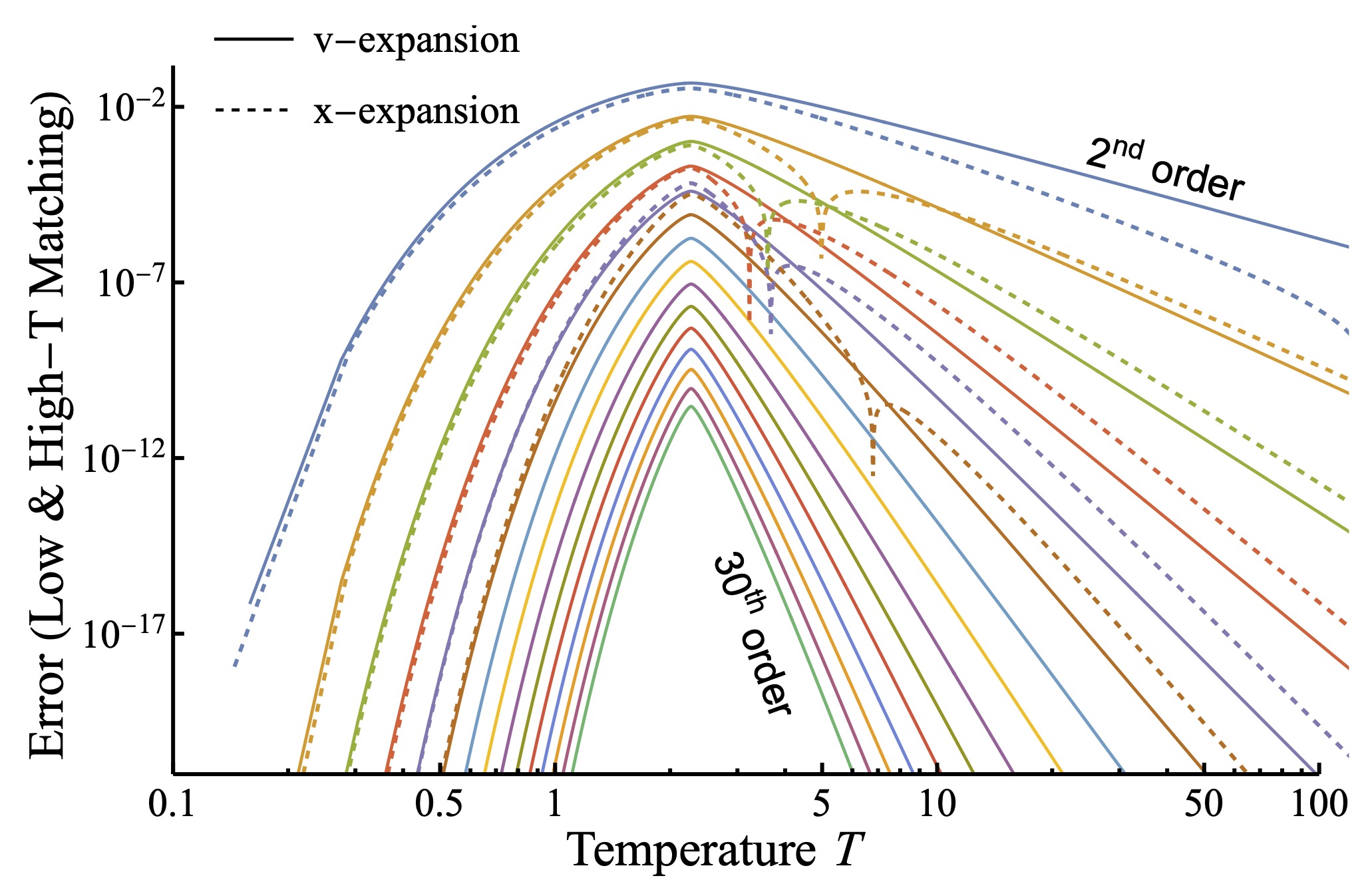
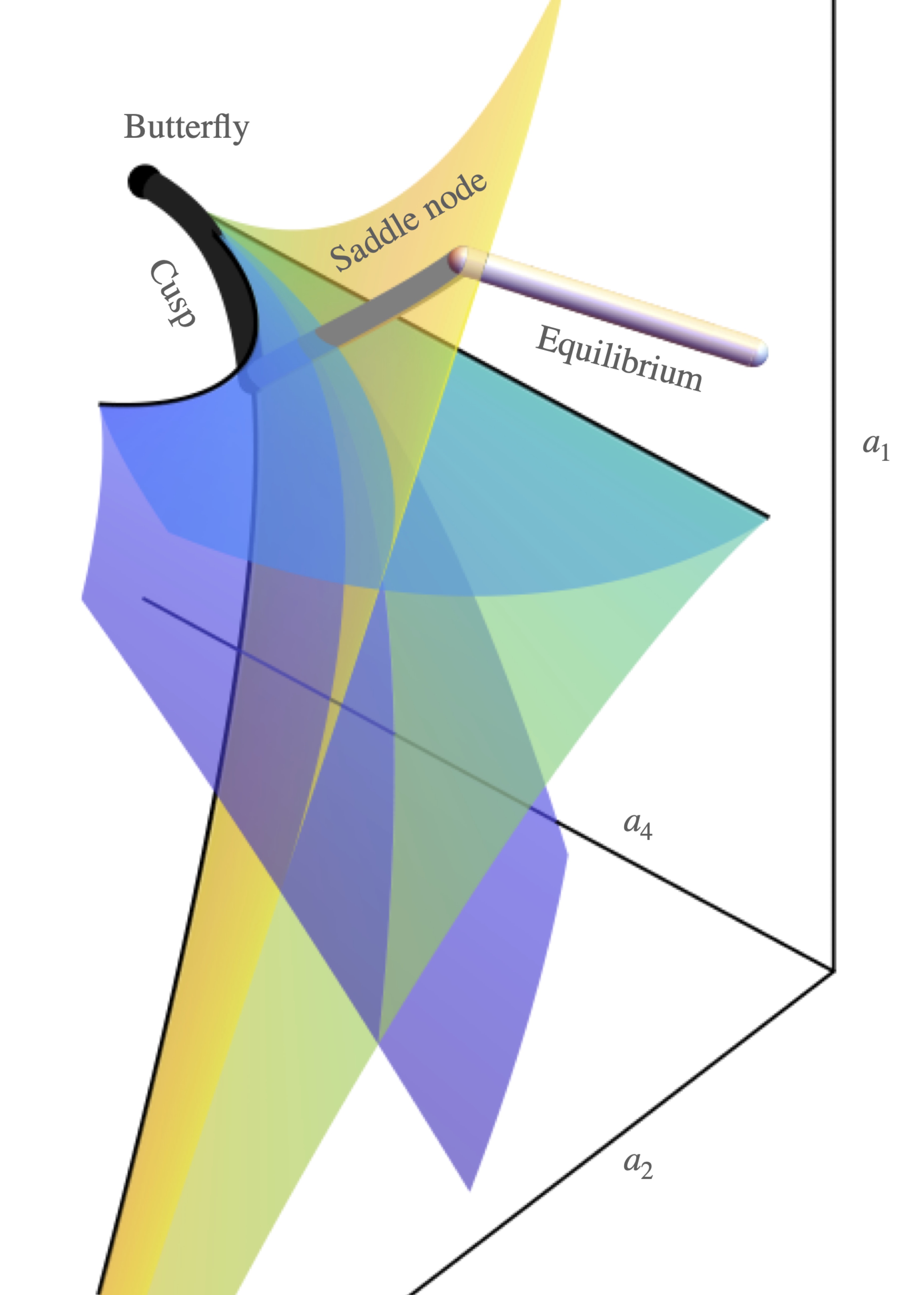
Another current research focus is nonequilibrium many-body systems: characterizing their phase transitions, scaling laws, and the behavior of dissipation rates near phase boundaries. We aim to understand how nonequilibrium driving enables new collective phases and response properties that are not possible in equilibrium systems that satisfy the fluctuation-dissipation theorem. Our work both addresses these questions using both classical approaches and through the development of novel analytical and computational techniques.
Read more:
- D. Hathcock and J.P. Sethna, "Phase transitions beyond criticality: extending Ising universal scaling functions to describe entire phases," submitted, arXiv:2402.18531. [PDF]
- J.P. Sethna, D. Hathcock, J. Kent-Dobias, and A. Raju, "Normal forms, universal scaling functions, and extending the validity of the RG," in 50 Years of the Renormalization Group: Dedicated to the Memory of Michael E Fisher, World Scientific (2024). [PDF]
- T. Yang*, D. Hathcock*, Y. Chen, P. McEuen, J.P. Sethna, I. Cohen, and I. Griniasty, "Bifurcation instructed design of multistate machines," Proc. Natl. Acad. Sci. 120, e2300081120 (2023). [PDF] [SI]
- S. Chandra, D. Hathcock, K. Crain, T. Antonsen, M. Girvan, and E. Ott, "Modeling the network dynamics of pulse-coupled neurons," Chaos 27, 033102 (2017). [PDF]
First-Passage Problems and Birth-Death Processes
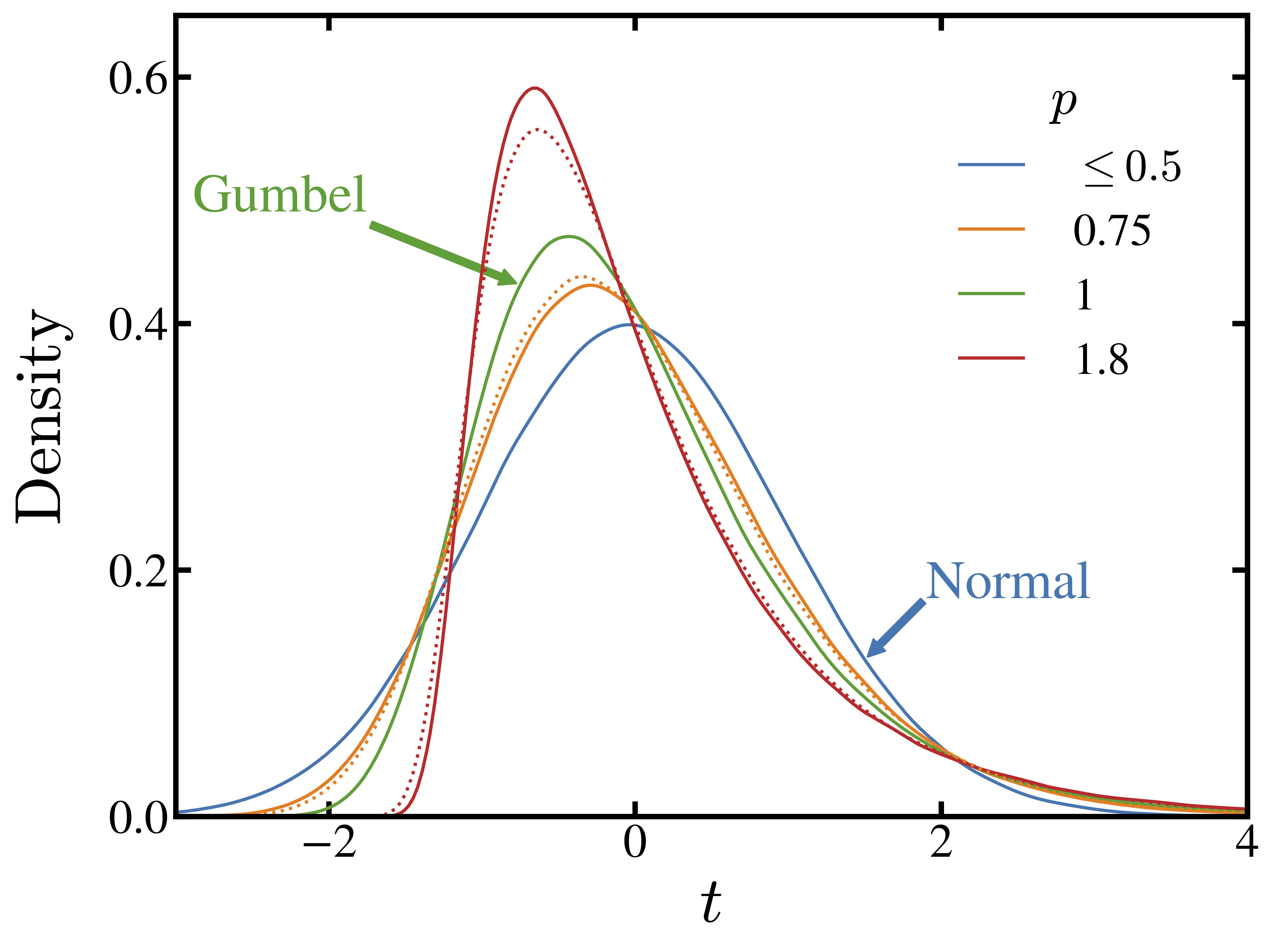
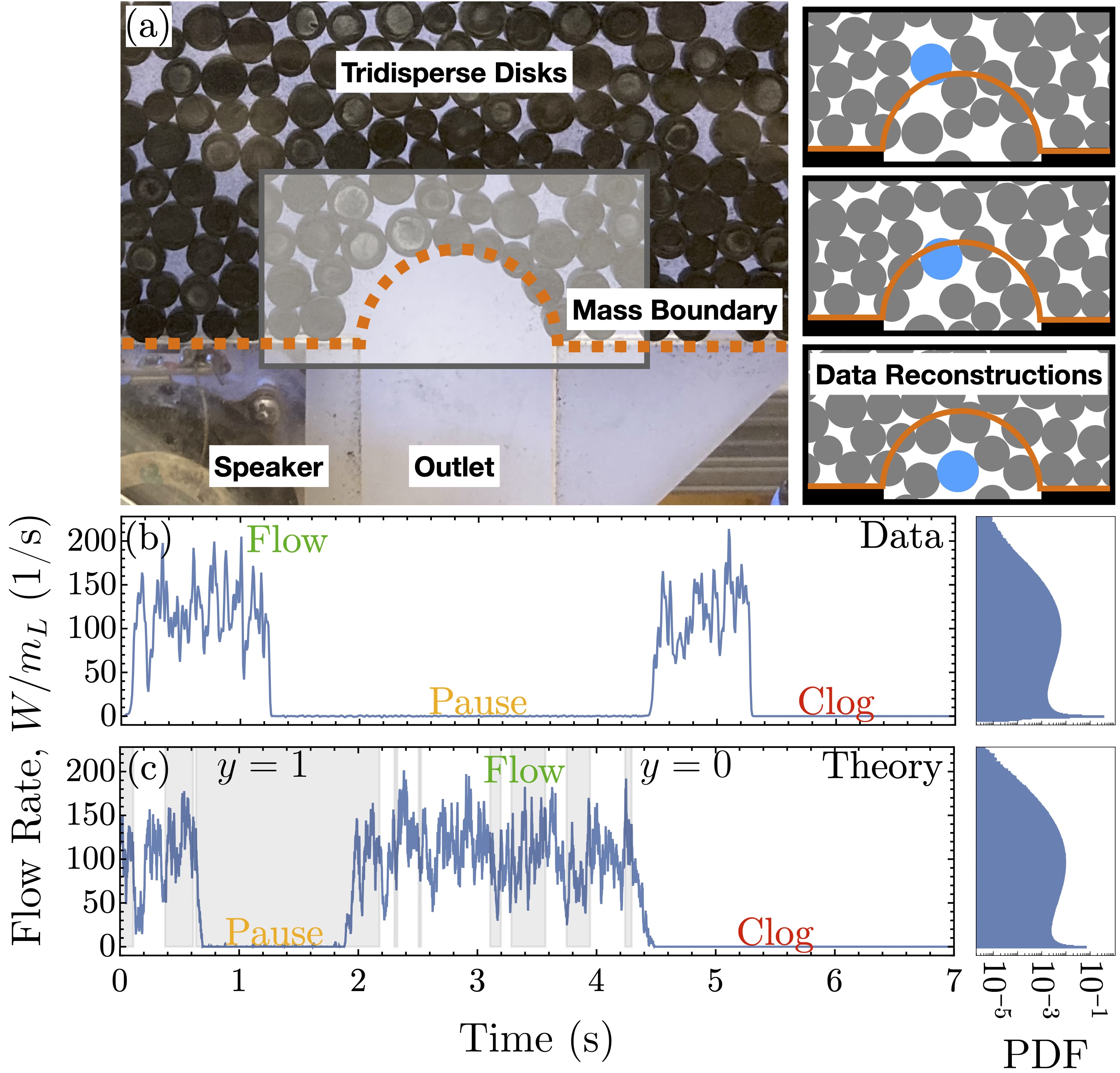
A broad range of biological and soft matter systems, from chemical reactions and gene expression to ecological, evolutionary, and epidemiological population dynamics, can be described by stochastic birth-death processes. Furthermore, many such systems have threshold or absorbing states, where the dynamics change dramatically or even halt entirely; hence the first-passage time to these states is central to understanding these systems. We have studied universal properties of first-passage processes: do common distributions or scaling laws arise based on generic features of the underlying dynamics? We have also used first-passage techniques to understand applications such as fixation in evolutionary dynamics and clogging in granular flows. Current research focuses on both advancing our theoretical understanding: characterizing recurrence probabilities and quasi-birth-death processes, and on biological applications: modeling stochasticity, correlations, and extrinsic heterogeneity in gene expression.
Read more:
- N.N Yehya, C.H Bohrer, Q. Yu*, D. Hathcock*, B. Goldberg, S. Leng, F. Harris, H. Hendrix, M. White, F. Leng, S. Meyer, Y. Tu, J. Xiao, "Chromosomal Topological Domain Formation Modulates Transcription and the Coupling of Neighboring Genes in Escherichia coli," submitted bioRxiv (2025). [PDF]
- D. Hathcock*, S. Dillavou*, J.H. Hanlan, D.J. Durian, and Y. Tu, "Stochastic dynamics of granular hopper flows: a configurational mode controls the stability of clogs," Phys. Rev. E. (Letter) 111, L023404 (2025). [PDF] [SI]
- D. Hathcock and S.H. Strogatz, "Asymptotic Absorption-Time Distributions in Extinction-Prone Markov Processes," Phys. Rev. Lett. 128, 218301 (2022). [PDF] [SI]
- D. Hathcock and J.P. Sethna, "Reaction rates and the noisy saddle-node bifurcation: Renormalization group for barrier crossing," Phys. Rev. Research 3, 013156 (2021). [PDF]
- D. Hathcock and S.H. Strogatz, "Fitness dependence of the fixation-time distribution for evolutionary dynamics on graphs," Phys. Rev. E 100, 012408 (2019). Featured as an Editors' suggestion. [PDF] [SI]
Molecular Biophysics
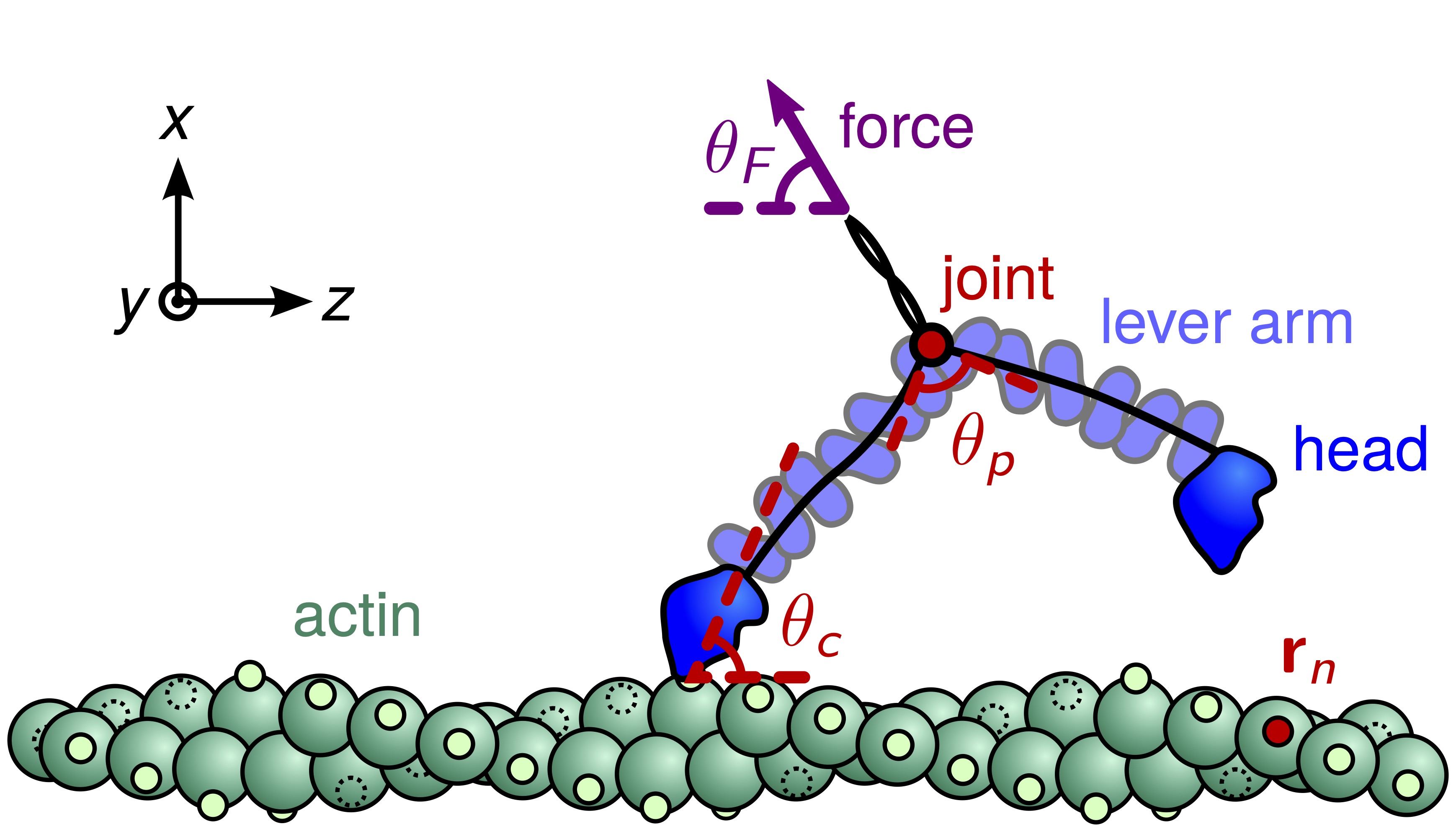
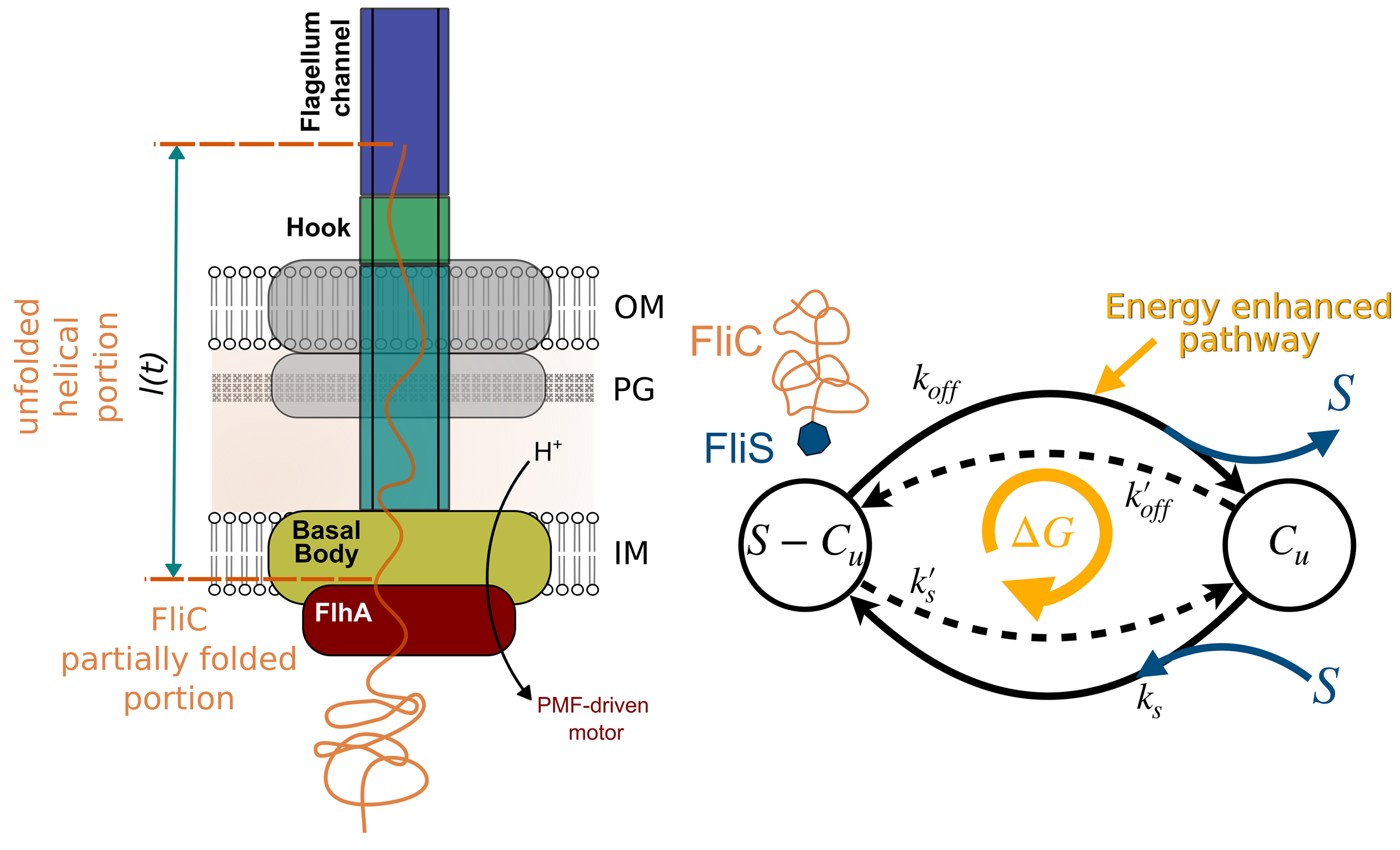
Outside of the above research themes, we have a range of ongoing and completed projects utilizing nonequilibrium statistical physics to study phenomena in molecular biophysics, including the stepping dynamics of molecular motors, the assembly of bacterial flagella, and chromosomal segregation during cell division.
Read more:
- M. Halte, P.F. Popp, D. Hathcock*, J. Severn*, S. Fischer, C. Goosmann, A. Ducret, E. Charpentier, Y. Tu, E. Lauga, M. Erhardt, and T.T. Renault, "Bacterial motility depends on a critical flagellum length and energy-optimised assembly," Proc. Natl. Acad. Sci. 122, e2413488122 (2025). [PDF] [SI]
- D. Hathcock, R. Tehver, M. Hinczewski, and D. Thirumalai, "Myosin V executes steps of variable length via structurally constrained diffusion," eLife 9, e51569 (2020). [PDF] [SI]